

Image Sampling with Quasicrystals
Web: www.Eyemaginary.com
Email: Mark@Eyemaginary.com
Citation:
Image Sampling with Quasicrystals
Mark Grundland, Jiri Patera, Zuzana Masakova, and Neil A. Dodgson
Symmetry, Integrability and Geometry: Methods and Applications (SIGMA), vol. 5, pp. 075:1-23, (2009). ISSN 1815-0659.
Presented also as a poster at the International Congress on Mathematical Physics (Prague, Czech Republic, 3-8 August, 2009).
Abstract:
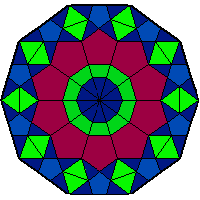
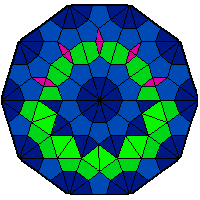
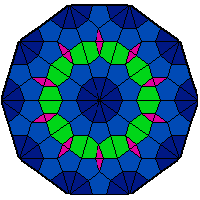
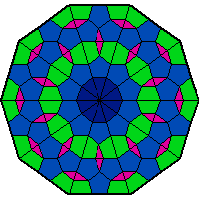
We investigate the use of quasicrystals in image sampling. Quasicrystals produce space-filling, non-periodic point sets that are uniformly discrete and relatively dense, thereby ensuring the sample sites are evenly spread out throughout the sampled image. Their self-similar structure can be attractive for creating sampling patterns endowed with a decorative symmetry. We present a brief general overview of the algebraic theory of cut-and-project quasicrystals based on the geometry of the golden ratio. To assess the practical utility of quasicrystal sampling, we evaluate the visual effects of a variety of non-adaptive image sampling strategies on photorealistic image reconstruction and non-photorealistic image rendering used in multiresolution image representations. For computer visualization of point sets used in image sampling, we introduce a mosaic rendering technique.
Online:
Paper + Experiments + Poster
Sampling Data: Periodic + Quasicrystal + Farthest Point + Jittered + Quasirandom + Random
Animations: Voronoi Diagram + Delaunay Graph + Delaunay Graph: The Sequel
Examples:
|
|||
| |
|||
|
Copyright © 2015 Mark Grundland. All rights reserved.